Nesse post trato de um algoritmo extremamente famoso: O algoritmo de Dijkstra.

NOTA: Este post foi publicado, originalmente, em 2016.

O que é?

Citando a wikipedia:

O algoritmo de Dijkstra, concebido pelo cientista da computação holandês Edsger Dijkstra em 1956 e publicado em 1959, soluciona o problema do caminho mais curto num grafo dirigido ou não dirigido com arestas de peso não negativo, em tempo computacional O([m+n]log n) onde m é o número de arestas e n é o número de vértices.

Um exemplo de problema resolvido por Dijkstra

Para que possamos ter um ponto de partida, assumamos o seguinte grafo:

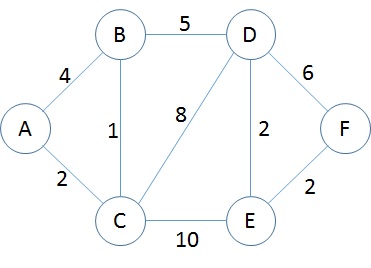
Considerando que os valores das arestas correspondem a uma distância, qual o caminho mais curto entre o vértice A e o vértice F?

Representando um grafo

Para que possamos implementar o algoritmo corretamente, comecemos definindo uma estrutura de classes para representar o nosso grafo.

public class Node
{
    public string Label { get; }
    public Node(string label)
    {
        Label = label;
    }

    readonly List _edges = new List();
    public IEnumerable Edges => _edges;

    public IEnumerable Neighbors =>
        from edge in Edges
        select new NeighborhoodInfo(
            edge.Node1 == this ? edge.Node2 : edge.Node1,
            edge.Value
            );

    private void Assign(Edge edge)
    {
        _edges.Add(edge);
    }

    public void ConnectTo(Node other, int connectionValue)
    {
        Edge.Create(connectionValue, this, other);
    }

    public struct NeighborhoodInfo
    {
        public Node Node { get; }
        public int WeightToNode { get; }

        public NeighborhoodInfo(Node node, int weightToNode)
        {
            Node = node;
            WeightToNode = weightToNode;
        }
    }

    public class Edge
    {
        public int Value { get; }
        public Node Node1 { get; }
        public Node Node2 { get; }

        public Edge(int value, Node node1, Node node2)
        {
            if (value <= 0)
            {
                throw new ArgumentException("Edge value needs to be positive.");
            }
            Value = value;
            Node1 = node1;
            node1.Assign(this);
            Node2 = node2;
            node2.Assign(this);
        }

        public static Edge Create(int value, Node node1, Node node2)
        {
            return new Edge(value, node1, node2);
        }
    }
}

A classe Node representa nossos vértices. A classe Edge representa nossas arestas.

A inicialização do grafo de exemplo seria realizada assim:

var a = new Node("A");
var b = new Node("B");
var c = new Node("C");
var d = new Node("D");
var e = new Node("E");
var f = new Node("F");

a.ConnectTo(b, 4);
a.ConnectTo(c, 2);
b.ConnectTo(c, 1);
b.ConnectTo(d, 5);
c.ConnectTo(d, 8);
c.ConnectTo(e, 10);
d.ConnectTo(f, 6);
d.ConnectTo(e, 2);
e.ConnectTo(f, 2);

Certo?

Abstraindo o problema que queremos resolver

Há diversos algoritmos para encontrar o caminho mais curto entre dois nodos. Por isso, resolvi resumir nosso problema com a seguinte abstração:

interface IShortestPathFinder
{
    Node[] FindShortestPath(Node from, Node to);
}

Basicamente, definimos uma função que retornará um vetor com o caminho a ser percorrido. Se não houver caminho possível, a função retornará null.

Implementando Dijkstra

Preparamos o terreno, agora, vamos a implementação.

public class Dijkstra : IShortestPathFinder
{
    private class Weight
    {
        public Node From { get; }
        public int Value { get; }

        public Weight(Node @from, int value)
        {
            From = @from;
            Value = value;
        }
    }

    class VisitingData
    {
        readonly List _visiteds =
            new List();

        readonly Dictionary<Node, Weight> _weights =
            new Dictionary<Node, Weight>();

        readonly List _scheduled =
            new List();

        public void RegisterVisitTo(Node node)
        {
            if (!_visiteds.Contains(node))
                _visiteds.Add((node));
        }

        public bool WasVisited(Node node)
        {
            return _visiteds.Contains(node);
        }

        public void UpdateWeight(Node node, Weight newWeight)
        {
            if (!_weights.ContainsKey(node))
            {
                _weights.Add(node, newWeight);
            }
            else
            {
                _weights[node] = newWeight;
            }
        }

        public Weight QueryWeight(Node node)
        {
            Weight result;
            if (!_weights.ContainsKey(node))
            {
                result = new Weight(null, int.MaxValue);
                _weights.Add(node, result);
            }
            else
            {
                result = _weights[node];
            }
            return result;
        }

        public void ScheduleVisitTo(Node node)
        {
            _scheduled.Add(node);
        }

        public bool HasScheduledVisits => _scheduled.Count > 0;

        public Node GetNodeToVisit()
        {
            var ordered = from n in _scheduled
                            orderby QueryWeight(n).Value
                            select n;

            var result = ordered.First();
            _scheduled.Remove(result);
            return result;
        }

        public bool HasComputedPathToOrigin(Node node)
        {
            return QueryWeight(node).From != null;
        }

        public IEnumerable ComputedPathToOrigin(Node node)
        {
            var n = node;
            while (n != null)
            {
                yield return n;
                n = QueryWeight(n).From;
            }
        }
    }

    public Node[] FindShortestPath(Node @from, Node to)
    {
        var control = new VisitingData();

        control.UpdateWeight(@from, new Weight(null, 0));
        control.ScheduleVisitTo(@from);

        while (control.HasScheduledVisits)
        {
            var visitingNode = control.GetNodeToVisit();
            var visitingNodeWeight = control.QueryWeight(visitingNode);
            control.RegisterVisitTo(visitingNode);

            foreach (var neighborhoodInfo in visitingNode.Neighbors)
            {
                if (!control.WasVisited(neighborhoodInfo.Node))
                {
                    control.ScheduleVisitTo(neighborhoodInfo.Node);
                }

                var neighborWeight = control.QueryWeight(neighborhoodInfo.Node);

                var probableWeight = (visitingNodeWeight.Value + neighborhoodInfo.WeightToNode);
                if (neighborWeight.Value > probableWeight)
                {
                    control.UpdateWeight(neighborhoodInfo.Node, new Weight(visitingNode, probableWeight));
                }
            }
        }

        return control.HasComputedPathToOrigin(to)
            ? control.ComputedPathToOrigin(to).Reverse().ToArray()
            : null;
    }
}

A classe VisitingData foi uma “opção de design”. Escolhi não sujar a estrutura de dados do grafo com informações identificando se um nodo foi ou não visitado, nem com valores intermediários produzidos pelo algoritmo.

A ideia do algoritmo se aproxima muito de uma BFS. Percorremos todos os vértices do grafo, partindo do vértice de origem, atualizando o peso relativo dos vizinhos de cada elemento para o início do caminho (mantendo sempre o peso mais baixo). Além disso, agendamos uma visita para cada um desses “vizinhos” que será realizada primeiro naqueles com menor “valor”. Importante observar que tomamos o cuidado de não visitar um mesmo vértice duas vezes. No final do processo, o vértice destino terá a menor distância possível para o vértice de início. Além disso, terá uma referência para seu antecessor.

BTW, a saída desse programa é: